在本文中，我们将探索如何使用基于 Signed Distance Function (SDF) 的技术来创建和渲染 3D 融球角色如星之卡比或者史莱姆。我们将详细讨论以下关键技术点： 1.使用光线步进（Ray Marching）技术实现融球隐式表面 2.利用指数对数函数构建的平滑最小值函数实现形状间的融合 3.应用有限差分方法（Finite Difference）生成法线 4.实现深度写入
1. 使用光线步进（Ray Marching）技术实现融球隐式表面
// 球体的距离场函数
float4 sphereDistanceFunction(float4 sphere, float3 pos)
{
return length(sphere.xyz - pos) - sphere.w;
}
在以下的 HLSL 代码示例中，我们定义了一个球体的距离场函数，其中sphere.xyz表示球体的位置，sphere.w是球体的半径，而 pos 是当前光线步进的位置。
// 返回与所有球体的最短距离
float getDistance(float3 pos)
{
float dist = 100000;
for (int i = 0; i < _SphereCount; i++)
{
dist = smoothMin(dist, sphereDistanceFunction(_Spheres[i], pos), 15);
}
return dist;
}
我们使用getDistance函数来计算从光线当前位置到隐式表面融球的最短距离。这通过遍历所有球体并应用 smoothMin函数来实现平滑的融合效果。
for (int i = 0; i < 20; i++)
{
// pos与融球整体的最短距离
float dist = getDistance(pos);
// 沿射线方向前进
pos += dist * rayDir;
}
此循环体中，光线从世界空间像素坐标出发，沿着摄像机到当前像素的方向逐步前进，直到达到迭代次数上限（20次）。每次循环时首先计算当前位置与融球体的最短距离，然后沿该方向步进相应距离。
这时候对于这个像素来说可以获得的结果举例有如上图所示：
A:dist值很大甚至大于1
B:dist很小趋近于0
当然这只是两个比较极端的结果，举出来是方便理解，输出所有的dist值可以直观的看到结果，dist的作用是区分出融球实体部分，为其写入深度，颜色和法线作准备。
2. 利用指数对数函数构建的平滑最小值函数实现形状间的融合
float smoothMin(float x1, float x2, float k)
{
return -log(exp(-k * x1) + exp(-k * x2)) / k;
}
功能：
对输入的x1，x2值提供一个平滑过渡的方式确定他们之间的较小值。确定最小值我们比较常用的是Min函数，但是它会有一个突变点，而smoothMin函数能提供一个平滑的曲线。
效果：
当k值接近于0时，平滑效果最明显，接近在x1和x2之间的软最小值。
当k值较大时，结果趋近于传统的min(x1,x2)函数。
3. 基于有限差分法（Finite Difference）的法线生成
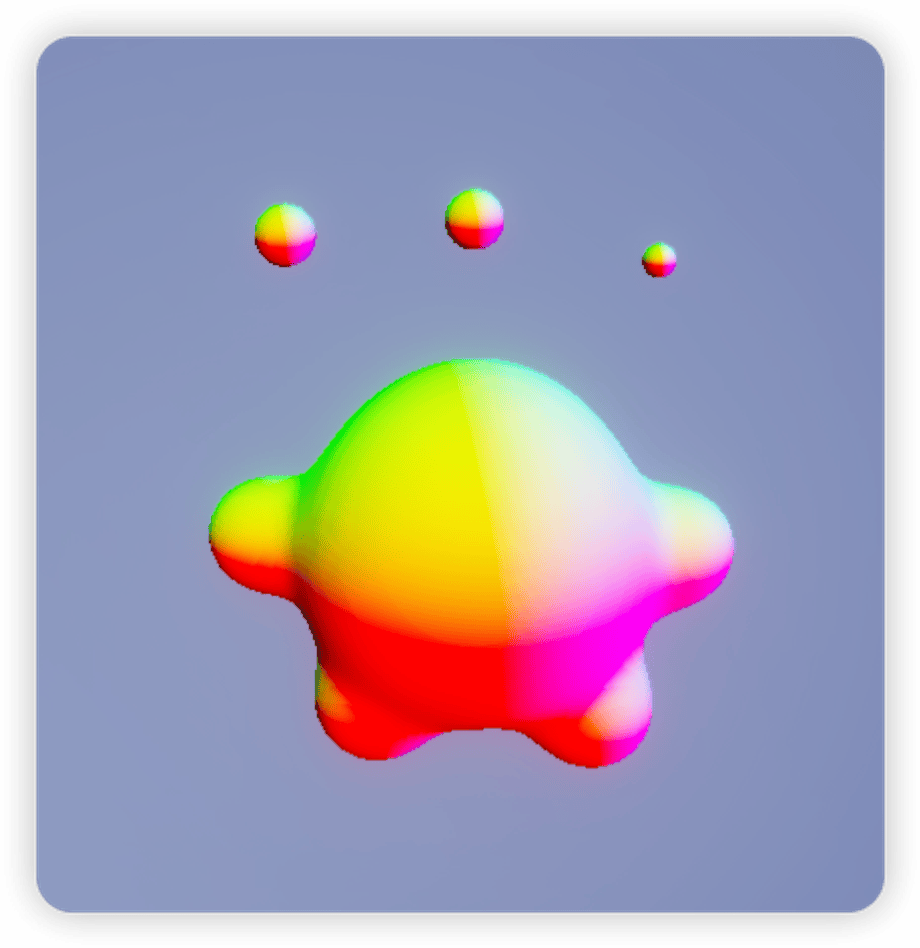
// 计算法线
float3 getNormal(float3 pos)
{
float d = 0.0001;
return normalize(float3(
getDistance(pos + float3(d, 0.0, 0.0)) - getDistance(pos + float3(-d, 0.0, 0.0)),
getDistance(pos + float3(0.0, d, 0.0)) - getDistance(pos + float3(0.0, -d, 0.0)),
getDistance(pos + float3(0.0, 0.0, d)) - getDistance(pos + float3(0.0, 0.0, -d))
));
}
使用中心差分方法来估算形状函数在 x、y、z 三个方向上的偏导数,
将这些导数构成一个向量。即可得到未归一化的法线向量n：
最后，归一化词向量得到单位法线向量
由于我们只需要取得方向向量，所以在程序中可以省略掉除以2d的计算。
功能：
输入形状上的点P的坐标(AX,AY),和最小差分的值d，分别计算x和y方向上的变化率，再将两个向量相加再做归一化得到法线向量。
效果：
d值的效果在shader中呈现出来的现象是0.0001时这种微小的偏移会使法线计算准确，但是在ggb中需要d值很大才会有比较精确的效果，所以d值在函数中对结果到底起到了什么影响作用呢？
有一种可能在ggb中过小的d值导致法线不精确是精度问题。
函数图形如上图所示，以xy二维平面举例
4. 实现深度写入
// 计算深度
inline float getDepth(float3 pos)
{
const float4 vpPos = mul(UNITY_MATRIX_VP, float4(pos, 1.0));
float z = vpPos.z / vpPos.w;
#if defined(SHADER_API_GLCORE) || \
defined(SHADER_API_OPENGL) || \
defined(SHADER_API_GLES) || \
defined(SHADER_API_GLES3)
return z * 0.5 + 0.5;
#else
return z;
#endif
}
将RayMarching击中融球体的像素位置坐标从世界空间转换到观察空间，除以的vpPos.w值获得透视变化后的深度z。再匹配不同图形接口的深度值范围。
output frag(Varyings i)
{
output o;
......
for (int i = 0; i < 20; i++)
{
float dist = getDistance(pos);
......
if(dist < 0.01)
{
......
o.depth = getDepth(pos); // 写入深度
}
// 沿射线方向前进
pos += dist * rayDir;
}
// 如果没有发生碰撞，则设置为透明
o.col = 0;
o.depth = 0;
return o;
}
在循环体中，每次迭代都会检测是否发生碰撞，若光线步进的位置与融球形状的最短距离小于0.01，则写入深度值，否则深度保持为 0。这样确保了只有当光线确实击中目标物体时，才记录深度信息。 在下篇中将详细讲解各种融球材质效果的实现以及工程链接。
5. 参考
- 这个大佬实现了简单易懂的融球液体 [https://qiita.com/yuyu0127/items/6976c2be84875610b310]
- 由顽皮狗大佬开发，功能完整的融球插件 [https://assetstore.unity.com/packages/tools/particles-effects/mudbun-volumetric-vfx-modeling-177891]
